Matemática 3°1°
Profe: Cintia Brizuela
mail: cintiambrizu@gmail.com
Hola chicos! como están!!Espero que muy bien. Seguimos trabajando con los números racionales y las expresiones decimales.
Como ya mencionamos anteriormente:
Todo número racional puede expresarse en base decimal. Esta expresión es, por decirlo coloquialmente, lo que la mayoría de gente entiende por un número con coma.
Veamos qué queremos decir con el siguiente ejemplo,
Ejemplo
El número racional 1/2
Y entonces leemos cero coma cinco en vez de un medio.
Esta expresión es útil si nos estamos refiriendo, por ejemplo a un precio o longitud, donde es necesario hacerse una idea del valor del número racional.
Esta expresión en base decimal no puede ser siempre exacta ya que por ejemplo 1/3=0.33333333...
Siempre que digamos periódico nos referiremos a que el número debe ser repetido infinitas veces. La parte periódica la simbolizamos con una barra sobre el numero en cuestión o un arco.
Ahora, ¿Como pasamos de decimales periódicos puros a fracción?
Observa como ejemplo el número
Paso 1: Reescribe el número
Escribe el número con la notación resumida de la barra en la cola decimal. En este caso en lugar de escribir se escribe: .
Paso 2: El numerador
El numerador de la fracción será el número decimal escrito sin coma y sin barra, menos la parte entera del mismo, en este caso:
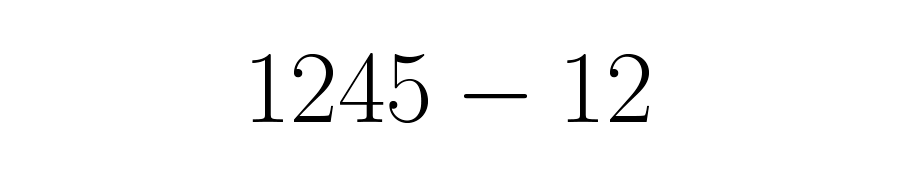
Paso 3: El denominador
El denominador será un número con tantos nueves como cifras decimales tenga el número original en su notación de barra.
Como tiene dos cifras periódicas en su cola decimal, el y el , se deben poner dos nueves como denominador. Recuerda que en este paso siempre se usa el número .
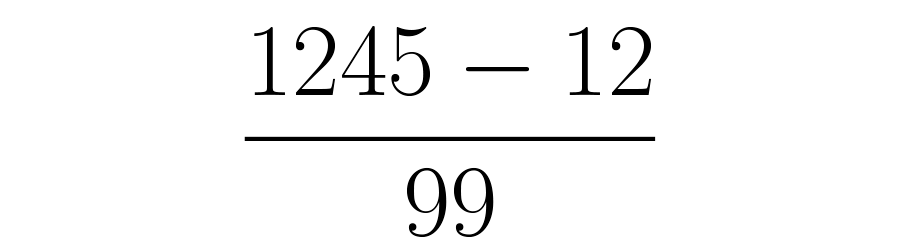
Paso 4: Realizar las operaciones
Ahora se resta y simplifica: en esta ocasión se debe realizar la resta: , obteniendo la fracción . Al simplificar esta misma da como resultado .
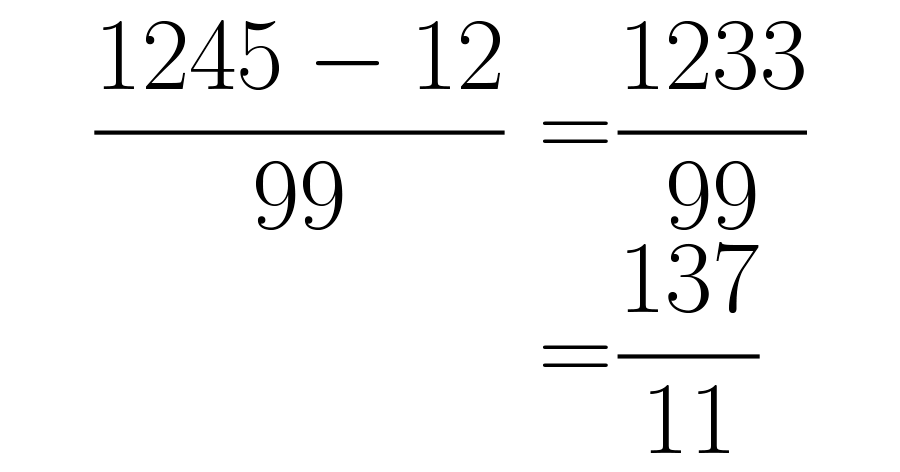
Si realizas la división , encontrarás que su resultado es Lo anterior quiere decir que .
Otro ejemplo
Observa un ejemplo más interesante: encontremos una fracción que represente el decimal
Paso 1:
Se escribe el número con la notación de barra:
Paso 2:
El numerador será el número escrito sin coma y sin barra, menos la parte entera del mismo número. Recuerda que
Paso 3.
El denominador será tantos nueves como cifras decimales periódicas tenga el número original. En este caso hay solamente una cifra decimal periódica, por lo tanto el denominador tendrá un solo nueve.
Paso 4:
Para finalizar se realiza la resta y se simplifica. Al simplificar la
Para finalizar se realiza la resta y se simplifica. Al simplificar la fracción se obtiene como resultado .
Observa el procedimiento completo en la siguiente imagen:
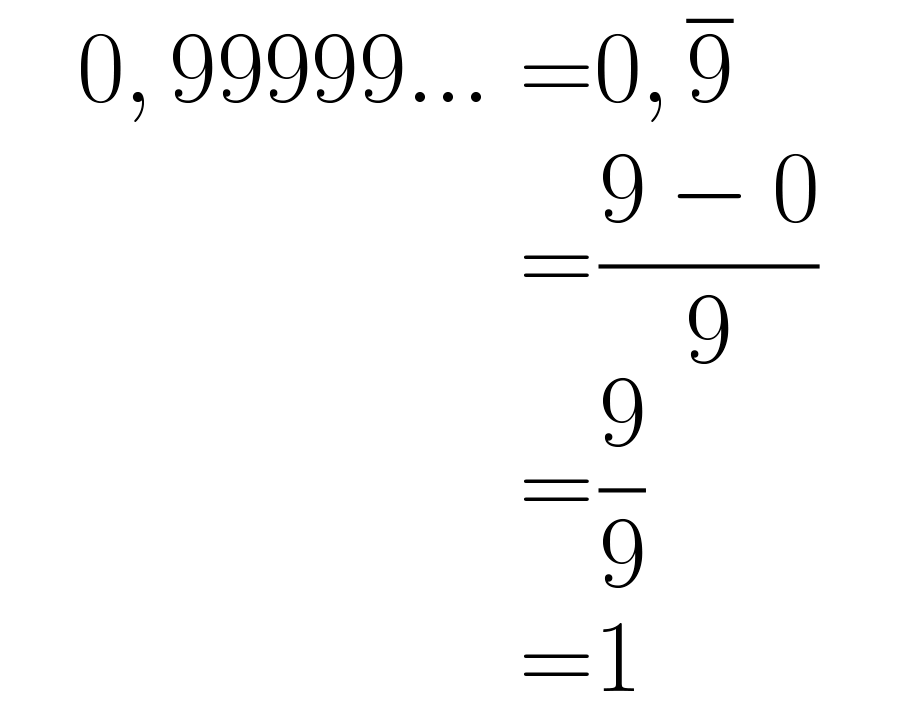



No hay comentarios.:
Publicar un comentario